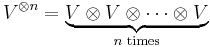Faithful representation

In mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ(g).

In more abstract language, this means that the group homomorphism

ρ: G → GL(V)

is injective.

Caveat: While representations of G over a field K are de facto the same as $K[G]$ -modules (with $K[G]$ denoting the group algebra of the group G), a faithful representation of G is not necessarily a faithful module for the group algebra. In fact each faithful $K[G]$ -module is a faithful representation of G, but the converse does not hold. Consider for example the natural representation of the symmetric group S_n in n dimensions by permutation matrices, which is certainly faithful. Here the order of the group is n! while the n×n matrices form a vector space of dimension n². As soon as n is at least 4, dimension counting means that some linear dependence must occur between permutation matrices (since 24 > 16); this relation means that the module for the group algebra is not faithful.

Properties

A representation V of a finite group G over an algebraically closed field K of characteristic zero is faithful (as a representation) if and only if every irreducible representation of G occurs as a subrepresentation of SⁿV (the n-th symmetric power of the representation V) for a sufficiently high n. Also, V is faithful (as a representation) if and only if every irreducible representation of G occurs as a subrepresentation of

$V^{\otimes n}=\underbrace{V\otimes V\otimes \cdots\otimes V}_{n\text{ times}}$

(the n-th tensor power of the representation V) for a sufficiently high n.

References

Hazewinkel, Michiel, ed. (2001), "faithful representation", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=F/f038170